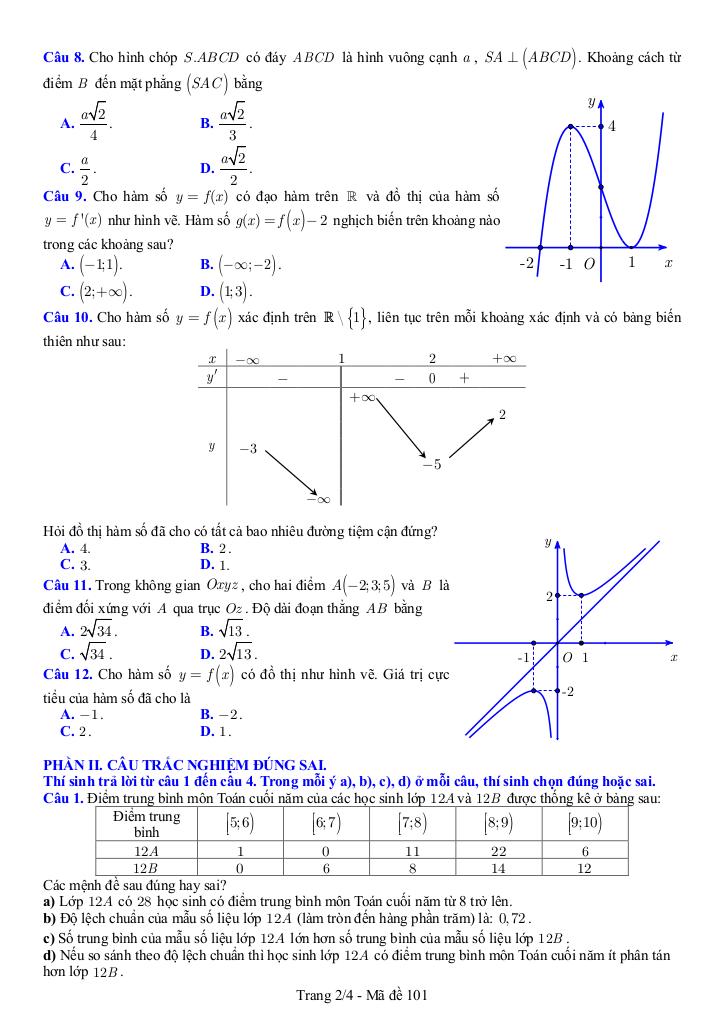
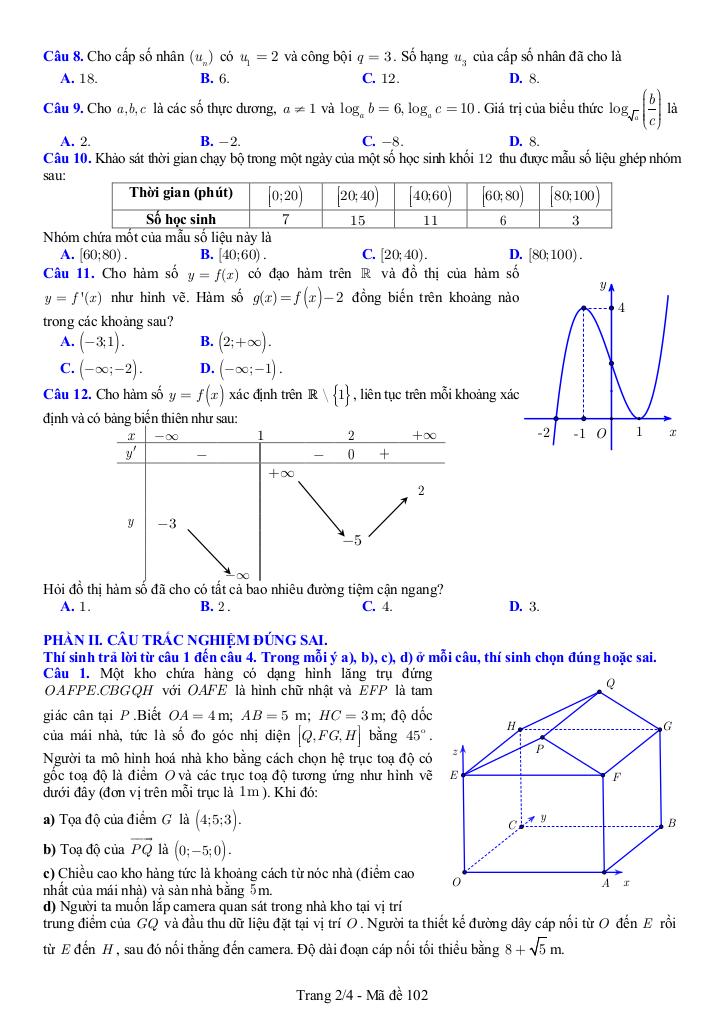
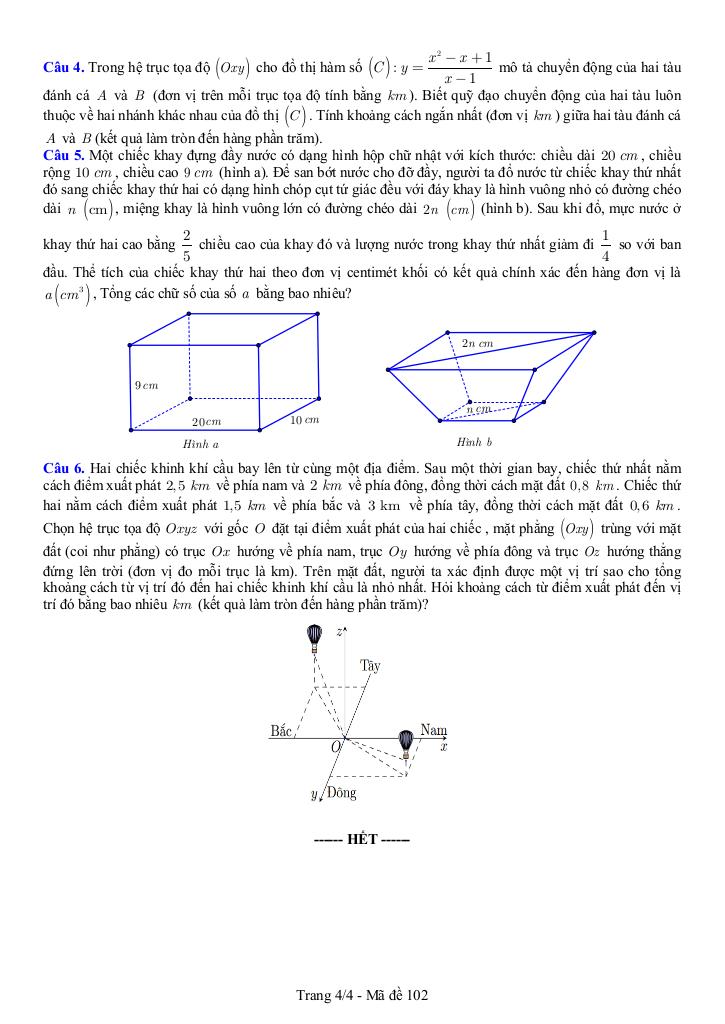
Đề khảo sát chất lượng môn Toán lớp 12 năm học 2024 – 2025 | Cụm các trường THPT và Trung tâm GDTX – Bắc Ninh

Montoan.com.vn trân trọng giới thiệu đến quý thầy cô và các em học sinh lớp 12 đề khảo sát chất lượng môn Toán lớp 12, năm học 2024 – 2025 của cụm các trường THPT, Trung tâm GDTX và GDNN – GDTX tại tỉnh Bắc Ninh. Kỳ thi được tổ chức vào Chủ Nhật, ngày 05 tháng 01 năm 2025, nhằm đánh giá toàn diện kiến thức và kỹ năng của học sinh, hướng đến kỳ thi tốt nghiệp THPT quốc gia. Đề thi có đáp án chi tiết (mã đề 101 và 102), là tài liệu ôn tập cần thiết để chuẩn bị cho kỳ thi quan trọng.

Cấu trúc và nội dung đề khảo sát chất lượng Toán 12

1. Bài toán hình học không gian: Tìm khoảng cách tối thiểu

Đề bài:

Hai chiếc flycam được điều khiển bay lên cùng lúc từ một địa điểm.

• Flycam thứ nhất bay đến điểm \(A\) (cách mặt đất 5 m, cách điểm xuất phát 3 m về phía nam và 2 m về phía đông).
• Flycam thứ hai bay đến điểm \(B\) (cách mặt đất 5 m, cách điểm xuất phát 6 m về phía bắc và 6 m về phía tây).

Sử dụng hệ trục tọa độ \(Oxyz\):

• \[ O: \text{Điểm xuất phát}. \].
• \[ Ox: \text{Hướng nam}. \].
• \[ Oy: \text{Hướng đông}. \].
• \[ Oz: \text{Hướng thẳng đứng lên}. \].

Yêu cầu:

Tìm vị trí trên mặt đất sao cho tổng khoảng cách từ vị trí này đến hai chiếc flycam là nhỏ nhất và tính khoảng cách từ điểm xuất phát đến vị trí đó.

Hướng dẫn giải:

1. Xác định tọa độ hai điểm:
   • Điểm \(A\): \[ A(3, 2, 5) \], Điểm \(B\): \[ B(-6, -6, 5) \].
2. Sử dụng công thức tìm điểm trên mặt phẳng \(Oxy\) sao cho tổng khoảng cách tối thiểu.
3. Kết quả cuối cùng: Khoảng cách từ điểm xuất phát đến vị trí đó là: \[ 6 \, \text{mét}. \]

2. Bài toán xác suất: Tính xác suất dự án trúng thầu

Đề bài:

Một công ty đấu thầu 3 dự án \(X\), \(Y\), \(Z\) với xác suất trúng thầu lần lượt là: \[ X: a, \quad Y: b, \quad Z: 0,8. \]. Điều kiện: \[ a /> b. \]

• Xác suất để ít nhất một dự án trúng thầu là: \[ P(\text{ít nhất một dự án trúng thầu}) = 0,964. \]
• Xác suất để cả ba dự án đều trúng thầu là: \[ P(\text{cả ba dự án trúng thầu}) = 0,224. \]

Yêu cầu:

Tính \(2a + b\), biết rằng ba sự kiện trúng thầu của \(X\), \(Y\), \(Z\) là độc lập.

Hướng dẫn giải:

1. Sử dụng công thức xác suất:

   \[ P(\text{ít nhất một dự án trúng}) = 1 - P(\text{không dự án nào trúng}) \]

   \[ P(\text{ít nhất một dự án trúng}) = 1 - (1 - a)(1 - b)(1 - 0,8). \]

2. Dựa vào điều kiện \(P(XYZ) = 0,224\) để thiết lập phương trình.
3. Tìm \(a\) và \(b\) từ hệ phương trình, sau đó tính: \[ 2a + b. \]
4. Kết quả cuối cùng: \[ 2a + b = 1,8. \].

3. Bài toán lợi nhuận lớn nhất: Công ty xây dựng

Đề bài:

Một nhà máy \(A\) sản xuất tối đa \(100 \, \text{tấn sản phẩm/tháng}\) với giá bán mỗi tấn được biểu diễn bởi:

\[ P(x) = 50 - 0,001x^2 \, (\text{triệu đồng/tấn}), \] trong đó \(x\) là số tấn sản phẩm được sản xuất,

chi phí sản xuất:

\[ C(x) = 95 + 35x \, (\text{triệu đồng}), \] trong đó \(x\) là số tấn sản phẩm được sản xuất.

Yêu cầu:

Tìm lợi nhuận lớn nhất mà nhà máy có thể đạt được trong một tháng, làm tròn đến hàng triệu đồng.

Hướng dẫn giải:

1. Công thức lợi nhuận:

   \[ L(x) = P(x) \cdot x - C(x), \]

2. Khai triển và đơn giản hóa biểu thức:

   \[ L(x) = (50 - 0,001x^2)x - (95 + 35x), \].

3. Lấy đạo hàm \(L'(x)\) và tìm giá trị \(x\) tại điểm cực đại.
4. Kiểm tra điều kiện để xác định giá trị \(x\) tối ưu.
5. Kết quả cuối cùng: \[ \text{Lợi nhuận lớn nhất là } 1.230 \, \text{triệu đồng}. \]

Chiến lược ôn tập hiệu quả

1. Nắm vững kiến thức trọng tâm

• Hình học không gian: Sử dụng tọa độ và các công thức khoảng cách trong không gian 3 chiều.
• Xác suất: Hiểu rõ các công thức xác suất độc lập và có điều kiện.
• Đạo hàm và ứng dụng: Áp dụng đạo hàm để giải các bài toán tối ưu hóa.

2. Thực hành bài tập đa dạng

• Luyện tập các bài toán mô phỏng thực tế để tăng kỹ năng phân tích và giải quyết vấn đề.
• Thực hành đề thi thử để làm quen với cấu trúc và áp lực thời gian.

3. Phân tích đáp án

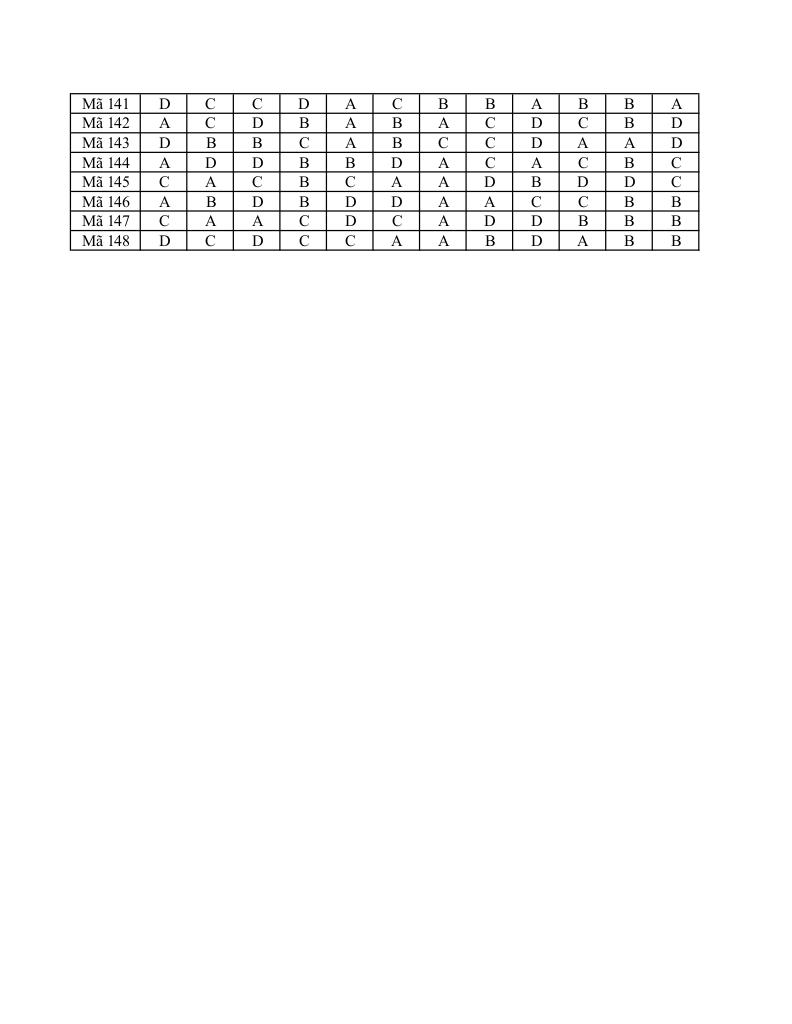
• Đối chiếu bài làm với đáp án mã đề 101 và 102 để rút kinh nghiệm từ lỗi sai.

Tải đề thi và đáp án

Truy cập Montoan.com.vn để tải về đề khảo sát chất lượng môn Toán 12 năm học 2024 – 2025 kèm đáp án chi tiết. Đây là nguồn tài liệu chất lượng, giúp học sinh ôn tập hiệu quả và chuẩn bị tốt cho kỳ thi tốt nghiệp THPT.

Lời kết

Đề khảo sát chất lượng môn Toán 12 tại cụm các trường THPT tỉnh Bắc Ninh là cơ hội để học sinh rèn luyện kỹ năng và kiến thức toàn diện. Chúc các em đạt được kết quả xuất sắc trong kỳ thi!